The wireless communication channel usually spans several physical “dimensions” such as space, time, frequency, polarization, etc. Numerous works have successfully used tensor decompositions as a mathematical formalism to describe the algebraic structure of the wireless channel.
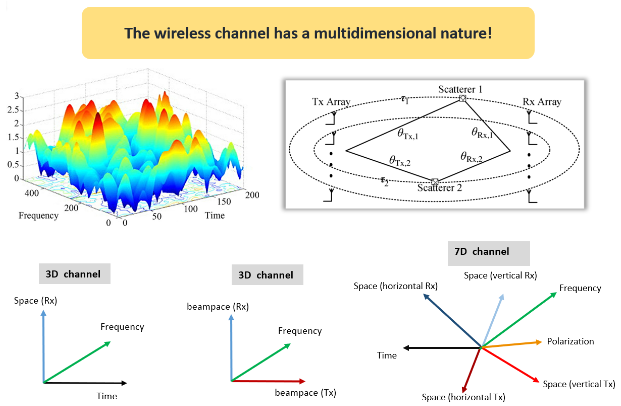
Figure 3: The physical dimensions of wireless communication channels lead to a multidimensional structure.
Tensor decompositions have recently been exploited to model and estimate mmWave channels, assuming hybrid analog-digital architectures. Leveraging tridimensional sparse representations of the large-scale channel matrices, tensor compressive sensing (tensor-CS) methods can effectively estimate the channel parameters by compressively sampling them in space (radio-frequency chains), time (symbol periods) and frequency (pilot subcarriers).
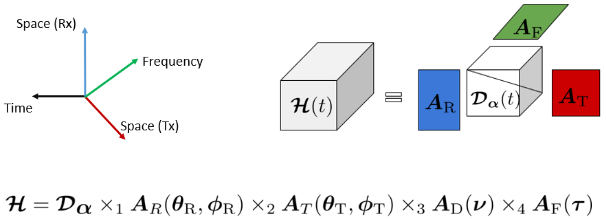
Figure 4: PARAFAC/CPD decomposition of the space-time-frequency MIMO channel.
Alternatively, the wireless channel can be algebraically represented with tensor train representations, where the higher-order tensor channel is decomposed into third-order smaller tensors (each one being a “wagon” of the tensor train). The tensor train approach significantly reduces the number of channel coefficients estimated by exploiting the low-rank channel structure if available. This is particularly useful when dealing with large-scale and structured MIMO channels in higher frequency bands.
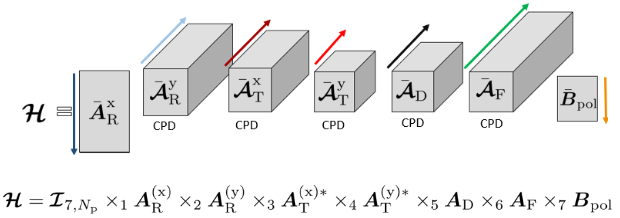
Figure 5: Tensor-train decomposition of a 7D large-scale MIMO channel into CPD tensor blocks.
Key points:
- Realistic channel models are highly structured in different domains
- Algebraic channel structure is heterogeneous in different domains (space, frequency, time, polarization, etc.)
- Multidimensional channel structure is lost when working with vectorized (or “matricized”) versions of the communication channel
[1] D. C. Araújo, A. L. F. de Almeida, J. P. C. L. da Costa, R. T. de Sousa Jr., “Tensor-based channel estimation for massive MIMO-OFDM systems,” IEEE Access, vol. 7, pp. 42133-42147, 2019.
[2] B. Sokal, P. R. B. Gomes, A. L. F. de Almeida, M. Haardt, “Tensor-based semi-blind receiver for joint channel, data, and phase noise estimation in frequency-selective MIMO systems”, IEEE Journal of Selected Topics in Signal Processing, vol. 15, pp. 803-815, 2021.
[3] Y. Znyed, R. Boyer, A. L. F. de Almeida, G. Favier, “Multidimensional harmonic retrieval based on Vandermonde tensor train,” Signal Processing, vol. 163, pp. 75-86, 2019.
[4] D. C. Araújo, A. L. F. de Almeida, “Tensor-based compressed estimation of frequency-selective mmWave MIMO channels, The 7th IEEE Workshop on Computational Advances in Multisensor Adaptive Processing (CAMSAP), 2017, Curaçao, vol. 1. p. 1-5.


